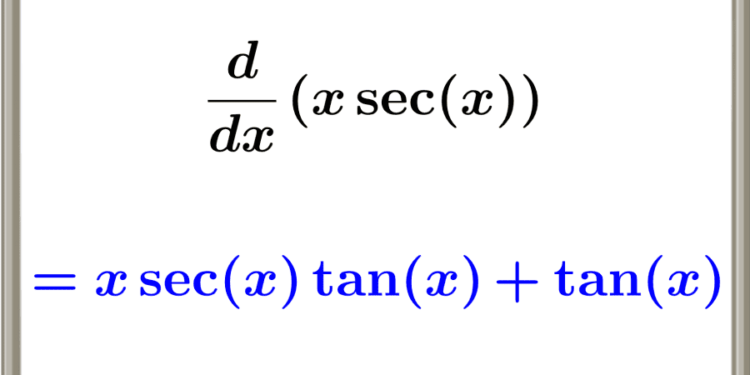Last Updated on September 1, 2022 by admin
Derivative of Secx
Derivative of Secx – To calculate the derivative of secx, we must first find its product. If sec 2 (x) is a product, then sec(x) is a derivative. Alternatively, we can use the chain rule to differentiate expressions in x. It is useful in cases where the function of x is not known but we know a derivative of sec(x).
tan x
The derivative of a function with one input value is the slope of the tangent line. A tangent point is a line that is the closest linear approximation of the function. This is also called the instantaneous rate of change. A derivative is the change in the dependent variable proportional to the change in the individual variable. Using the chain rule, tan x is the derivative of secx.
The tangent function has two parts: the cosecant and cot functions. The cotangent function connects the length of a side to its angle. In a right triangle, secX is the ratio of the hypotenuse to the adjacent side. Both secx and cot are derivatives of secx. Therefore, they are related. However, in the tangent function, the hypotenuse is longer than the adjacent side, so x > p is the derivative of secx.
Sec x
You’ve probably heard of the Sec x derivative. But what is it? What is the first principle of the Sec x derivative? How do you calculate it? Here are some examples. To begin, let’s define sec x. A secant function has one integral, and two products. These products can be expressed as an expression in any one or more variables. To find the Sec x derivative, start by calculating the exponent of the secant function.
You can also use the quotient rule to find the secant function. This rule originates from the relation sec(x) = 1/cos(x). The quotient rule is used to find the Sec X derivative. It can be expressed as dfracd or secd, depending on the variable you’re working with. The Sec x derivative can be expressed in any way that relates to the variable.
Sec 2 x
The secant squared function is the secant squared function x2. You can find the secant squared function’s derivative by applying the chain rule. This rule is used to differentiate expressions in x. Its derivative equals two sec2x times tanx. This is the definition of sec2x derivative. Here are some examples of derivatives. The first example is the secant squared function x2.
The second example shows how to find the derivative of sec2x. If x is an angle, then the secant squared function is the secant squared function. Then, if x is a function of a third variable, then the secant squared function is the derivative of sec2x. In order to solve this problem, you must multiply x with a power of 2.
Sec 3 x
The first principle of calculus is used to find the derivative of a function. The derivative of a function is the product of its first and second derivatives. The derivative of a function can also be expressed as the product of its sec, tan, and x. We can calculate the sec of a function by dividing the value of x by tan, which gives us 2x sec x2 tan x2.
In addition, the derivative of a function is another function. The derivative is the limit of change of the function with respect to its input. The first derivative of a function is the secant of its x-th derivative. If the second derivative of a function is greater than its first derivative, it is the secant of x-th power. In the second derivative, x-th power is less than x.
Sec 4 x
The Sec 4 x derivative rule comes from the relation sec(x) = 1/cos(x). The first step is to use the quotient rule, which states that (fg)’=f’g+f’g’. This rule will lead you to the Sec 4 x derivative. But how do you find the derivative of Sec 4 x? Let’s see. Here are some examples of how to find the Sec 4 x derivative.
The first principle of calculus is used to find the derivative of functions. This principle helps us find the slope and the area of a curve. However, the Sec 4 x derivative has a much simpler form. It can be written as sec2x. Alternatively, Sec 2 x can be written as sec(x).
Sec 5 x
A Sec 5 x derivative is a function of the angle. Using the same angle, f(x) is a function of x. If we change the angle and use a different variable, f(t) is a function of y. In this article, we will not look at implicit differentiation, but the answer should be the same as the previous one. This article will not cover implicit differentiation in detail, so let’s just keep the answer simple.
A Sec 5-x derivative is the product of a secant function and a tangent function with respect to x. It can be found using the first principle of differentiation and the limits operation form. There are several different ways to differentiate a Sec 5 x function, but all of them are based on the same concept. This article will provide some examples of how the two types of derivatives are derived. Once you understand how to differentiate a Sec 5 x function, you’ll be well on your way to solving problems in mathematics.
Sec 6 x
The secant of an angle is called a f(x) derivative. It is a function of the same angle. By extension, f(x) is also known as f(xi). The product rule states that f(x)’=f(xi+1). The power rule is another way to define the derivative as a function of an angle. Trigonometric differentiation is a method of determining the secant of a function of two variables.
Sec 7 x
The Sec 7 x derivative is an extension of the tangent line. Hence, f(x) is equivalent to secx. Another variant of this derivative is called the secxtanx. It has the same properties as the Sec 7 x derivative, except that the exponent is always higher. Here’s how it works. Using this formula, you can solve problems involving secxtanx.
First, you need to know the product of the secant and tangent functions of a given variable. You can write these two functions in trigonometric notation. Then, take their derivative in terms of the variable. In a similar way, you can write a secant function as (sec x)’ and the tangent as (tan x).
Sec 8 x
What is a sec 8 x derivative? This is the derivative of a tangent line. The secant line is also known as the tangent function, but that name is not immediately obvious. We will define a sec 8 x derivative using the following method. Firstly, the derivative of a secant line is the tangent of x times the sine of x. Then we can denote a derivative of a secant line as the secxtanx.
Sec 12 x
The second derivative of a function f(x) is a number whose value is equal to its second derivative. The second derivative may be expressed in radians, degrees, or grades. A secant calculator lets you enter the angle and choose the unit you need to calculate in. After you click calculate, you will see the result. The secant function also recognizes special angles. Here are a few examples of its uses: